Procesamiento de señales: Filtro de media móvil exponencial (EMA)

Anteriormente, en Introducción al procesamiento de señales, hemos visto las dos clases de filtros: Respuesta de impulso finito (FIR) y Respuesta de impulso infinito (IIR). Vimos cómo el filtro de la media móvil se puede expresar tanto en forma FIR como IIR, pero ¿cuáles son los beneficios de uno sobre el otro?

Si volvemos al ejemplo de mi blog anterior, el filtro FIR expandido tiene la forma:

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1]+x[0])/5,

Aquí, necesitamos:

1. 5 multiplicación y
2. 4 operaciones de sumatoria.

Las operaciones de multiplicación son especialmente costosas desde el punto de vista computacional. Por lo tanto, si volvemos a mirar el formulario IIR, vemos que solo requiere:

1. 3 multiplicación y
2. 2 operaciones de sumatoria.

y[6]=(x[6]+y[5]-x[1])/5

¡Esto reduce significativamente el costo de cálculo! Esto es bueno para los dispositivos integrados, como los microcontroladores, ya que gastan menos recursos en cada paso de tiempo discreto para realizar cálculos.

Por ejemplo, cuando uso la función de Python 'time.time' para el filtro de media móvil de 11 puntos en forma FIR e IIR, con todos los parámetros (tamaño de la ventana, frecuencia de muestreo, tamaño de la muestra, etc.) iguales, obtengo los siguientes resultados de tiempo de ejecución respectivamente: 51 ms, 27 ms.

Ejemplo de filtro IIR de tiempo discreto

Ahora que tenemos una intuición de por qué los filtros IIR funcionan mejor en microcontroladores, veamos un proyecto de ejemplo utilizando un Arduino UNO y una unidad de medición inercial (IMU) DFRobot MPU6050 (Figura 1). Aplicaremos el filtro de media móvil exponencial (EMA) a los datos de la IMU para ver las diferencias entre los datos brutos y los suavizados.

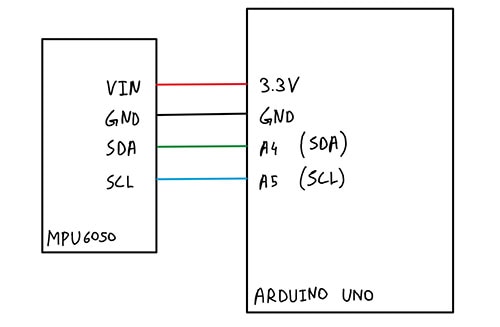Figura 1: Diagrama de bloques de conexión entre MPU6050 y Arduino Uno. (Fuente de la imagen: Mustahsin Zarif)

Figura 2: Conexión entre MPU6050 y Arduino Uno. (Fuente de la imagen: Mustahsin Zarif)

El filtro de media móvil exponencial es de la forma recursiva:

y[n] = α*x[n] + (1- α)*y[n-1]

Es recursivo porque cualquier salida de corriente que estemos midiendo también depende de las salidas anteriores; es decir, el sistema tiene memoria.

El alfa constante () determina cuánto peso queremos dar a la entrada actual en comparación con las salidas anteriores. Para mayor claridad, se expande la ecuación para obtener:

y[n] = α*x[n] + (1- α )*(α*x[n−1]+(1−α)*y[n−2])

y[n] = α*x[n] + (1- α )*x[n−1]+α*(1−α)2*x[n−2])+ ...

y[n] = k=0nα*(1−α)k*x[n−k]

Vemos que cuanto mayor es el alfa, más afecta la entrada de corriente a la salida de corriente. Esto es bueno ya que si el sistema está evolucionando, los valores del pasado no son tan representativos del sistema actual. Por otro lado, esto sería malo si, por ejemplo, hay un cambio repentino y momentáneo en el sistema de lo normal. En este caso, nos gustaría que nuestra salida siguiera la tendencia que seguían las salidas anteriores.

Ahora, sin más preámbulos, veamos cómo funcionaría el código para un filtro EMA para el MPU6050.

Código de filtro EMA:

Copy#include <wire.h>
#include <mpu6050.h>

MPU6050 mpu;

#define BUFFER_SIZE 11  // Window size

float accelXBuffer[BUFFER_SIZE];
float accelYBuffer[BUFFER_SIZE];
float accelZBuffer[BUFFER_SIZE];
int bufferCount = 0;  

void setup() {
  Serial.begin(115200);
  Wire.begin();

  mpu.initialize();

  if (!mpu.testConnection()) {
    Serial.println("MPU6050 connection failed!");
    while (1);
  }

  int16_t ax, ay, az;
  for (int i = 0; i < BUFFER_SIZE; i++) {
    mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);
    accelXBuffer[i] = ax / 16384.0;
    accelYBuffer[i] = ay / 16384.0;
    accelZBuffer[i] = az / 16384.0;
  }
  bufferCount = BUFFER_SIZE;
}

void loop() {
  int16_t accelX, accelY, accelZ;

  mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);

  float accelX_float = accelX / 16384.0;
  float accelY_float = accelY / 16384.0;
  float accelZ_float = accelZ / 16384.0;

  if (bufferCount < BUFFER_SIZE) {
    accelXBuffer[bufferCount] = accelX_float;
    accelYBuffer[bufferCount] = accelY_float;
    accelZBuffer[bufferCount] = accelZ_float;
    bufferCount++;
  } else {
    for (int i = 1; i < BUFFER_SIZE; i++) {
      accelXBuffer[i - 1] = accelXBuffer[i];
      accelYBuffer[i - 1] = accelYBuffer[i];
      accelZBuffer[i - 1] = accelZBuffer[i];
    }
    accelXBuffer[BUFFER_SIZE - 1] = accelX_float;
    accelYBuffer[BUFFER_SIZE - 1] = accelY_float;
    accelZBuffer[BUFFER_SIZE - 1] = accelZ_float;
  }

//calculate EMA using acceleration values stored in buffer
  float emaAccelX = accelXBuffer[0];
  float emaAccelY = accelYBuffer[0];
  float emaAccelZ = accelZBuffer[0];
  float alpha = 0.2;

  for (int i = 1; i < bufferCount; i++) {
    emaAccelX = alpha * accelXBuffer[i] + (1 - alpha) * emaAccelX;
    emaAccelY = alpha * accelYBuffer[i] + (1 - alpha) * emaAccelY;
    emaAccelZ = alpha * accelZBuffer[i] + (1 - alpha) * emaAccelZ;
  }

  Serial.print(accelX_float); Serial.print(",");
  Serial.print(accelY_float); Serial.print(",");
  Serial.print(accelZ_float); Serial.print(",");
  Serial.print(emaAccelX); Serial.print(",");
  Serial.print(emaAccelY); Serial.print(",");
  Serial.println(emaAccelZ);

  delay(100);
}
</mpu6050.h></wire.h>

Cuando ejecutamos este código y verificamos el trazador en serie, podemos ver líneas aproximadas y suaves en pares para aceleraciones en los ejes x, y y z, usando un tamaño de ventana de 11 y un valor alfa de 0.2 (Figura 3 a 5).

Figura 3: Valores de aceleración brutos y filtrados en la dirección x. (Fuente de la imagen: Mustahsin Zarif)

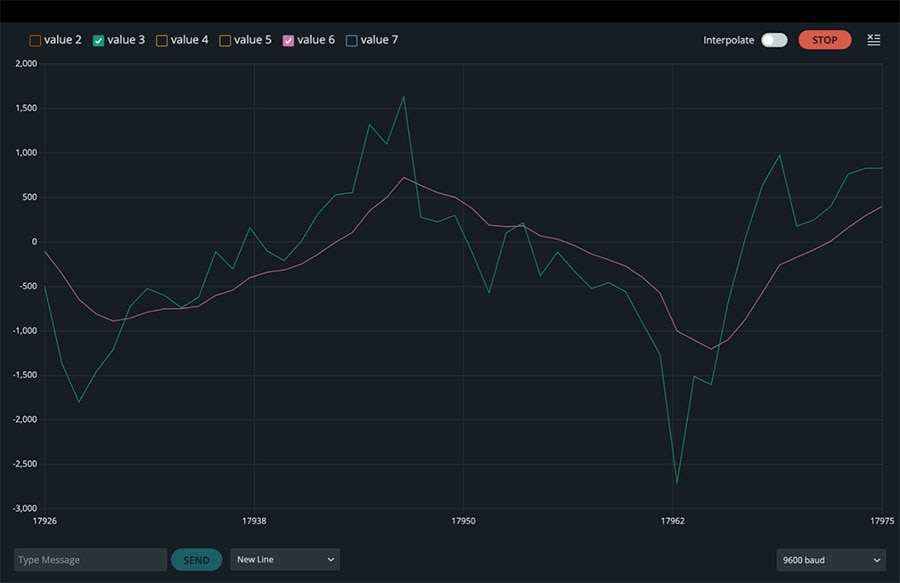Figura 4: Valores de aceleración brutos y filtrados en la dirección y. (Fuente de la imagen: Mustahsin Zarif)

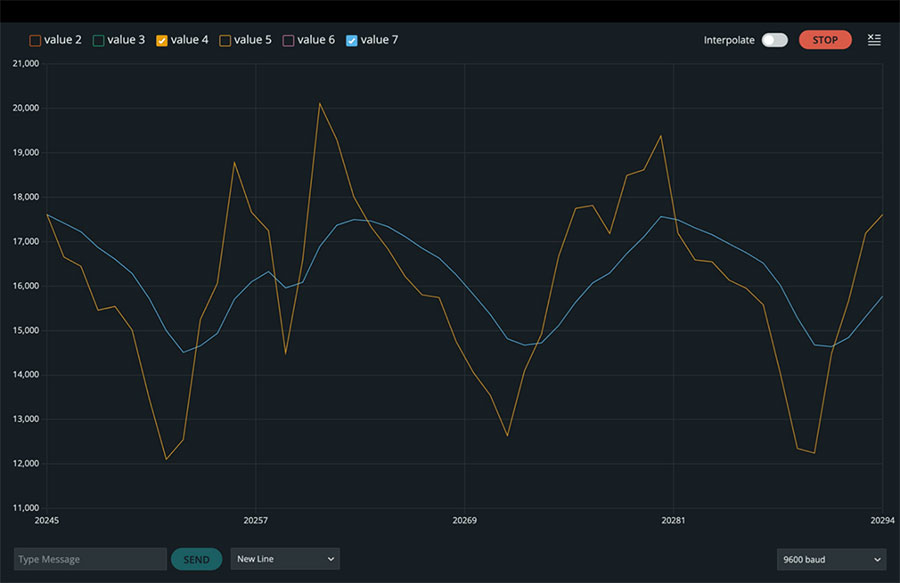Figura 3: Valores de aceleración brutos y filtrados en la dirección x. (Fuente de la imagen: Mustahsin Zarif)

Hacer que el código sea un paso más inteligente

Ahora tenemos una idea de cómo los filtros IIR son mejores para los controladores en comparación con los filtros FIR debido a los cálculos de suma y multiplicación significativamente menores requeridos. Sin embargo, cuando implementamos este código, la suma y la multiplicación no son los únicos cálculos que se realizan: tenemos que cambiar las muestras cada vez que entra una nueva muestra de tiempo, y este proceso, bajo el capó, requiere potencia de cálculo. Por lo tanto, en lugar de desplazar todas las muestras en cada intervalo de tiempo de muestreo, podemos emplear la ayuda de búferes circulares.

Esto es lo que hacemos: tenemos un puntero que recuerda el índice de la muestra de datos que entró. Luego, cada vez que el puntero apunta al último elemento del búfer, apunta al primer elemento del búfer a continuación, y los nuevos datos reemplazan los datos que se almacenaron aquí antes, ya que ahora son los datos más antiguos que ya no necesitamos (Figura 6). En consecuencia, este método nos permite realizar un seguimiento de la muestra más antigua en el búfer y reemplazarla sin tener que cambiar las muestras cada vez para colocar los nuevos datos en el último elemento de la matriz.

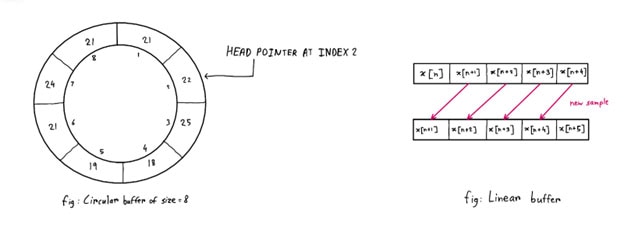Figura 6: Ejemplo de ilustración de un búfer circular. (Fuente de la imagen: Mustasin Zafir)

Este es el aspecto del código para una implementación de filtro EMA mediante búferes circulares. ¿Puedes intentar ejecutar esto para un giroscopio en lugar de un acelerómetro? ¡Juega también con los coeficientes!

Filtro EMA usando un código de búfer circular:

Copia#include <wire.h>

#include <mpu6050.h>

MPU6050 mpu;

#define BUFFER_SIZE 11  // Window size

float accelXBuffer[BUFFER_SIZE];

float accelYBuffer[BUFFER_SIZE];

float accelZBuffer[BUFFER_SIZE];

int bufferIndex = 0;  

void setup() {

  Serial.begin(115200);

  Wire.begin();
 

  mpu.initialize();


  if (!mpu.testConnection()) {

    Serial.println("MPU6050 connection failed!");

    while (1);

  }

  int16_t ax, ay, az;

  for (int i = 0; i < BUFFER_SIZE; i++) {

    mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);

    accelXBuffer[i] = ax / 16384.0;

    accelYBuffer[i] = ay / 16384.0;

    accelZBuffer[i] = az / 16384.0;

  }

}

void loop() {

  int16_t accelX, accelY, accelZ;

  mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);

  float accelX_float = accelX / 16384.0;

  float accelY_float = accelY / 16384.0;

  float accelZ_float = accelZ / 16384.0;

  accelXBuffer[bufferIndex] = accelX_float;

  accelYBuffer[bufferIndex] = accelY_float;

  accelZBuffer[bufferIndex] = accelZ_float;

  bufferIndex = (bufferIndex + 1) % BUFFER_SIZE; //circular buffer implementation 

  float emaAccelX = accelXBuffer[bufferIndex];

  float emaAccelY = accelYBuffer[bufferIndex];

  float emaAccelZ = accelZBuffer[bufferIndex];

  float alpha = 0.2;

  for (int i = 1; i < BUFFER_SIZE; i++) {

    int index = (bufferIndex + i) % BUFFER_SIZE;

    emaAccelX = alpha  accelXBuffer[index] + (1 - alpha)  emaAccelX;

    emaAccelY = alpha  accelYBuffer[index] + (1 - alpha)  emaAccelY;

    emaAccelZ = alpha  accelZBuffer[index] + (1 - alpha)  emaAccelZ;

  }

  Serial.print(accelX_float); Serial.print(",");

  Serial.print(emaAccelX); Serial.print(",");

  Serial.print(accelY_float); Serial.print(",");

  Serial.print(emaAccelY); Serial.print(",");

  Serial.print(accelZ_float); Serial.print(",");

  Serial.println(emaAccelZ);

  delay(100);

}
</mpu6050.h></wire.h>

Resumen

En este blog, discutimos la diferencia entre los filtros IIR y FIR con énfasis en sus eficiencias computacionales. Al tomar un pequeño ejemplo de la reducción en el número de operaciones requeridas de FIR a IIR, podemos imaginar cuán eficientes serán los filtros IIR cuando se escalen las aplicaciones, lo cual es importante para las aplicaciones en tiempo real con una potencia de hardware limitada.

También echamos un vistazo a un proyecto de ejemplo con un Arduino Uno e IMU MPU6050, en el que implementamos un filtro de media móvil exponencial para reducir el ruido en los datos del sensor sin dejar de capturar el comportamiento de la señal subyacente. Finalmente, en aras de la eficiencia, también vimos un ejemplo de código más inteligente mediante el empleo de búferes circulares en lugar de cambiar los datos en cada intervalo de tiempo.

¡En el próximo blog, usaremos la funcionalidad FPGA de Red Pitaya para implementar un circuito digital de filtro FIR de 4 toques!