Cómo realizar mediciones de respuesta de frecuencia rápidas y sencillas con un osciloscopio

¿Necesita comprobar la respuesta de frecuencia de un filtro o medir el ancho de banda de un amplificador? No es necesario tener una respuesta de frecuencia o un analizador de red. Puede calcular esa medida con un osciloscopio y una onda cuadrada con un flanco rápido.

Las mediciones de respuesta de frecuencia requieren una entrada con una amplitud constante en el rango de frecuencia de la medición. Los tres tipos de señales con un espectro de frecuencia plana son el barrido sinusoidal, el impulso y el ruido de banda ancha. De los tres, la respuesta de impulso produce el resultado más rápido. Entonces, la siguiente pregunta es: ¿cómo se obtiene una forma de onda de impulso?

Recuerde los conceptos básicos del análisis de circuitos: el impulso es la derivada de la función escalón. Si tiene la respuesta al escalón del dispositivo que está probando, puede convertirla en la respuesta de impulso diferenciándola. La mayoría de los osciloscopios de sobremesa incluyen integración y diferenciación como parte de sus paquetes de funciones matemáticas. En este ejemplo, se utiliza el osciloscopio Teledyne LeCroy HDO 4054A de 500 MHz (megahercios). El ancho de banda del osciloscopio debe exceder el del dispositivo que se mide por un factor de cinco para mantener los errores de amplitud sistemáticos por debajo de la mitad de un dB (decibelio). Un osciloscopio alternativo es el Teledyne LeCroy WAVESURFER-3054Z.

¿Cómo se obtiene una función escalón? Es fácil. El flanco ascendente o descendente aislado de una onda cuadrada o un pulso es una función escalón: diferenciar la función escalón produce un impulso. Esto se muestra en la Figura 1 para el flanco ascendente de una onda cuadrada de 10 kHz (kilohercios) (traza superior).

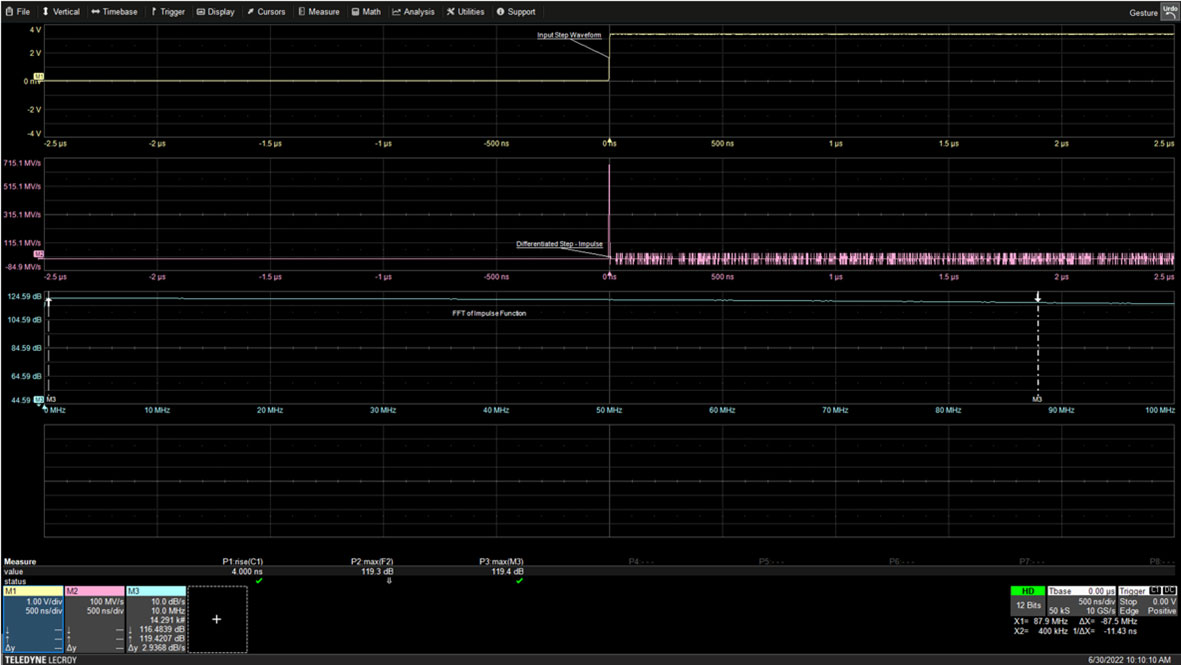Figura 1: El flanco ascendente de una onda cuadrada de 10 kHz se convierte en una función de impulso cuando se diferencia. El espectro del impulso es plano con un ancho de banda inversamente proporcional al tiempo de subida de la onda cuadrada. (Fuente de la imagen: Art Pini)

El osciloscopio captura solo 5 ms (microsegundos) alrededor del flanco. El equilibrio de la onda cuadrada de 100 ms está fuera de la pantalla. La función escalón se diferencia usando la capacidad matemática del osciloscopio y se muestra como la traza central. La FFT (transformada rápida de Fourier) del impulso se muestra en la traza inferior. El ancho de banda del impulso se determina por el tiempo de subida de la onda cuadrada. En este caso, el tiempo de subida se mide como 4 ns (nanosegundos), como se muestra en el parámetro de medición P1 debajo de las cuadrículas de traza. El ancho de banda del impulso se puede calcular como 0.35 dividido por el tiempo de subida para un osciloscopio con una respuesta de amplitud de un solo polo.

El resultado en este caso es 87.5 MHz, que está marcado por el cursor de la derecha en la pantalla FFT con una lectura numérica dentro del cuadro de anotación de la traza matemática M3. La amplitud de la FFT a 87.5 MHz es de 116.48 dB en comparación con la amplitud máxima de la FFT de 119.43 dB o, aproximadamente, -3 dB del máximo, lo que confirma el ancho de banda de la señal.

La fuente de señal para la medición de la respuesta de frecuencia debe ofrecer ondas cuadradas o formas de onda de pulso que sean lo suficientemente rápidas para proporcionar un ancho de banda de medición adecuado. El flanco de 4 ns utilizado en la figura fue generado por un generador de forma de onda arbitrario Teledyne LeCroy T3AWG2152-D de 150 MHz. Una fuente de señal con un tiempo de subida aún mayor de 2 ns es el Teledyne LeCroy T3AFG200, un generador de funciones arbitrarias de 200 MHz y 2.4 gigamuestras por segundo (Gmuestra/s). El tiempo de subida de 2 ns proporciona un ancho de banda de señal de 175 MHz.

Respuesta de frecuencia de un filtro de paso bajo digital

El siguiente ejemplo mide la respuesta de frecuencia de un filtro de paso bajo digital usando el osciloscopio Teledyne LeCroy HDO4054A y el T3AWG2152-D (Figura 2). Estas medidas de filtro aparecen en la columna de trazas de la izquierda.

La señal del escalón se aplica a la entrada del filtro. La salida del filtro se diferencia y se muestra. Tenga en cuenta que el filtro ha ampliado la respuesta de impulso debido a su ancho de banda limitado. La salida del filtro se aplica a la FFT y se promedia para producir la respuesta de frecuencia de magnitud del filtro.

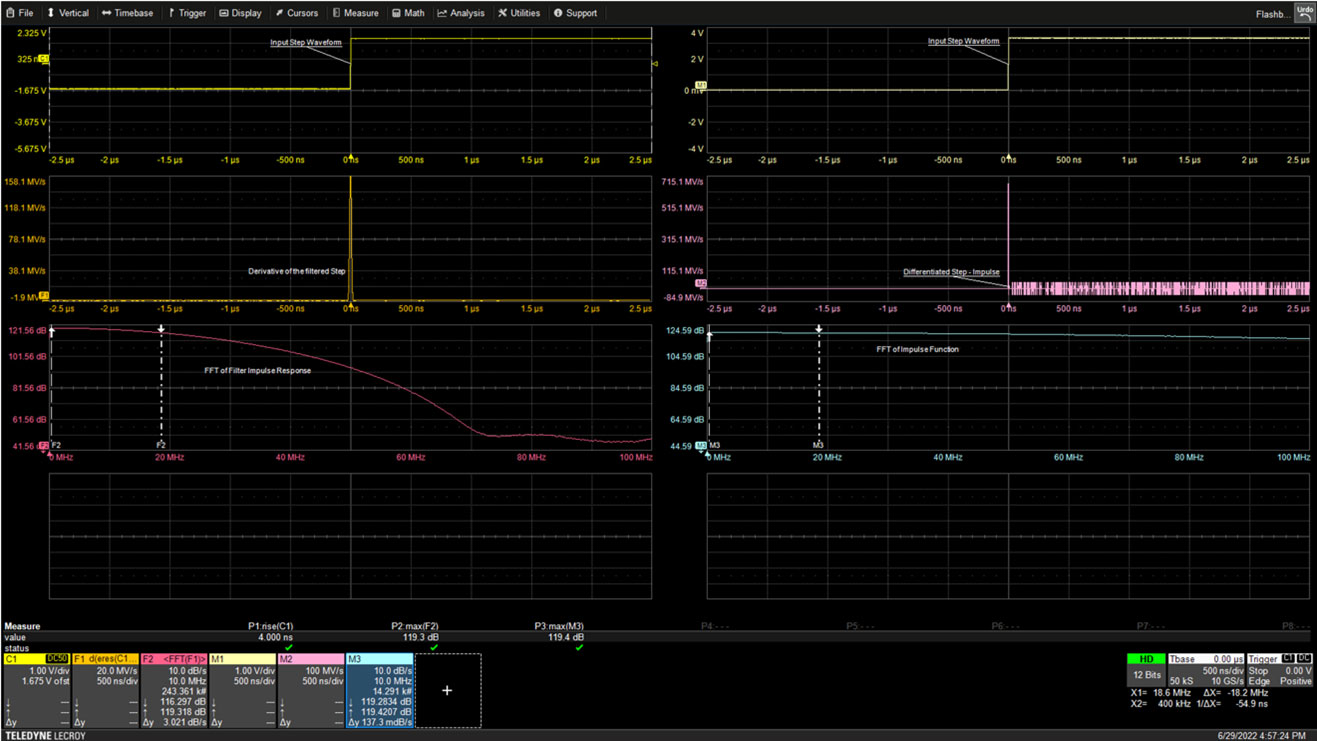Figura 2: La señal del escalón, la traza superior izquierda, se aplica a la entrada del filtro. La salida del filtro se diferencia y se muestra en la traza central izquierda. La FFT de la señal filtrada, la traza inferior izquierda, muestra la respuesta de frecuencia del filtro. (Fuente de la imagen: Art Pini)

Los cursores en la FFT de la salida del filtro leen el ancho de banda de -3 dB en el cuadro de anotación F2 a una frecuencia de 18.6 MHz. Este es el ancho de banda del filtro. Al mismo tiempo, el cursor en la FFT de la función de impulso en la traza inferior derecha muestra una atenuación de solo 0.12 dB en el cuadro de anotación M3 a 18.6 MHz. Esto indica que la fuente de la señal es básicamente plana.

Conclusión

Como se muestra, la respuesta de los componentes dependientes de la frecuencia se puede medir de manera fácil y rápida, sin recurrir a analizadores de red o de respuesta de frecuencia, con las funciones básicas del osciloscopio que operan en una onda cuadrada con un flanco rápido.